참고 :
이진 탐색 트리 (Binary Search Tree)
- 정의
효율적인 탐색, 빈번한 삽입과 삭제를 위해 이진 탐색(Binary Search)과 연결 리스트(Linked List)를 결합한 자료구조
평균 시간복잡도 : O(logN)
최악 시간복잡도 : O(N)
※
이진탐색 => 자료 입력, 삭제 불가능
연결리스트 => 자료 탐색 시 평균 시간복잡도 O(N)
- 이진 탐색

: 정렬된 배열 내 중간값과 찾고자 하는 값 비교를 반복, 탐색 범위를 절반씩 좁혀가며 찾고자 하는 값을 탐색함
시간복잡도 : O(logN)
=> 탐색할 때마다 절반씩 범위 좁혀짐
=> 자료 수가 2^n일 때 k번의 탐색으로 구하고자 하는 값 찾을 수 있음
ex. 16개 데이터 탐색
→ 8 (1차 : 16 * 1/2)
→ 4 (2차 : 16 * 1/2 * 1/2)
→ 2 (3차 : 16 * 1/2 * 1/2 * 1/2)
→ 1 (4차 : 16 * 1/2 * 1/2 * 1/2 * 1/2)
데이터 수 = 2^n * (1/2)^k
1 (최악의 경우) = 2^n * (1/2)^k
2^k = 2^n
k = logn
- 구조

각 노드의 왼쪽 서브트리 => 해당 노드 값보다 작은 값의 노드들로 이루어짐
각 노드의 오른쪽 서브트리 => 해당 노드 값보다 큰 값의 노드들로 이루어짐
중복된 노드가 없어야 함
왼쪽 서브트리, 오른쪽 서브트리 또한 이진탐색트리
=> 중위 순회 방식 사용 (왼쪽 서브트리 - 중간 노드 - 오른쪽 서브트리)
- 연산
- 검색

- 삽입
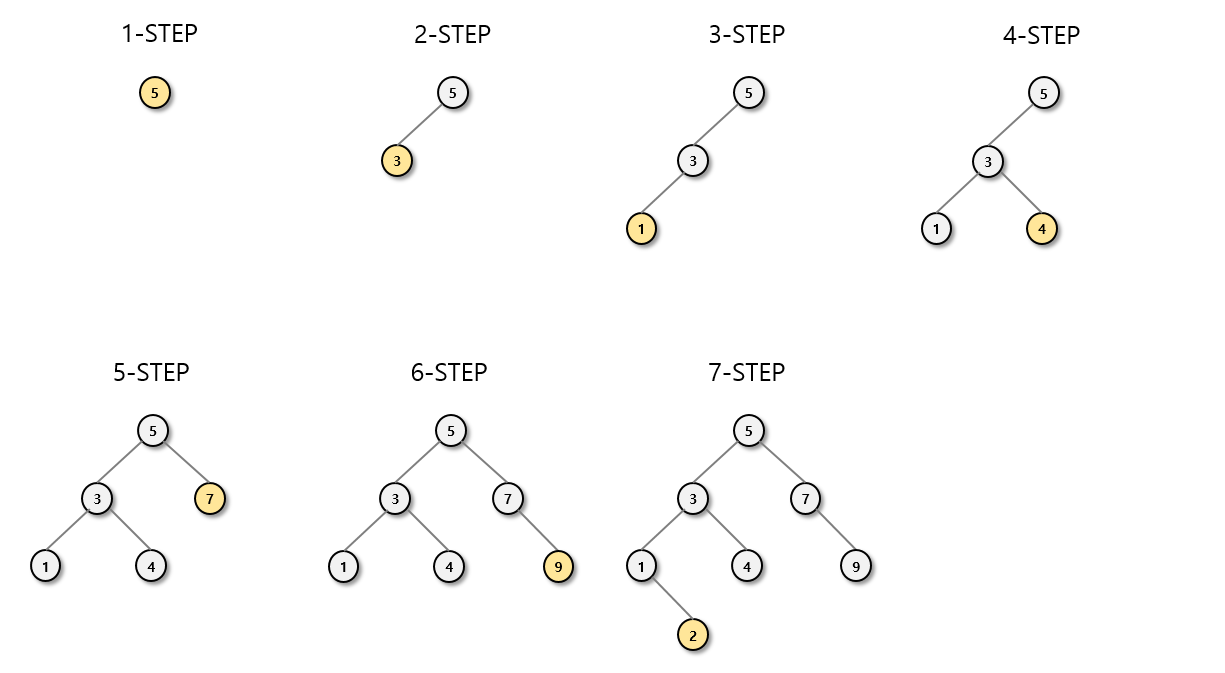
- 삭제
1. 삭제할 노드가 리프노드일 때 => 리프노드만 삭제
2. 삭제할 노드의 자식노드가 하나일 때 => 삭제노드 위치에 자식노드 대체
3. 삭제할 노드의 자식노드가 두개 이상일 때
=> 삭제할 노드의 왼쪽 서브 트리에서 최대값 노드 or 오른쪽 서브 트리에서 최소값 노드 구해 대체하기

- 한계

높이가 높은 불균형트리일 때 연산들의 성능이 악화됨 => O(h)
=> 삽입, 삭제 시 트리 전체의 균형을 맞추는 AVL Tree를 사용할 수 있음 (이진탐색트리의 일종)
'Programming > 알고리즘' 카테고리의 다른 글
| [자료구조] 우선순위 큐, 힙 (0) | 2023.06.16 |
|---|---|
| [백준/자바] 트리 1967번 - 트리의 지름 (0) | 2023.06.03 |
| [자료구조] 트리 - 이진 트리 유형 (0) | 2023.05.24 |
| [자료구조] 트리, 그래프 (0) | 2023.05.11 |
| DFS, BFS (0) | 2023.05.04 |



