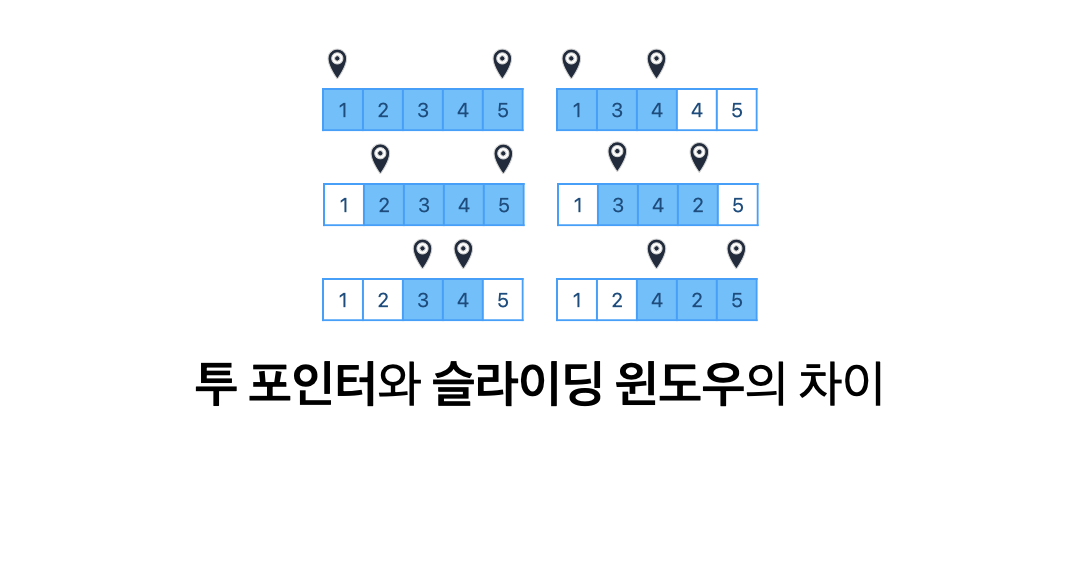
투 포인터와 슬라이딩 윈도우는 선형 공간 내 연속 구간에 대한 알고리즘이며, 주로 구간 합, 부분 수열의 합을 구하고 비교할 때 사용한다. 특히 1차원 배열을 2회 이상 탐색해야 할 때 시간 복잡도를 O(N^2)에서 O(N)으로 낮춰주는 특징이 있다.
다만 투 포인터는 start, end 포인터를 가변적으로 이동시키고, 슬라이딩 윈도우는 고정된 window 구간을 이동시킨다는 점에서 차이를 보인다. 처음 두 알고리즘을 접했을 땐 그 차이가 크게 다가오지 않았기 때문에 각 알고리즘에 대해 자세히 적어보고자 한다.
투 포인터
: 2개의 포인터(인덱스)를 이동시키며 값을 구하는 알고리즘

start와 end 포인터는 모두 인덱스 0에서 출발하거나, 각각 맨앞과 맨뒤 인덱스에서 시작한다.
구하고자 하는 값(ex. 누적합)을 증가시킬 땐 end 포인터를 우측 이동하여 해당 인덱스의 값을 누적시킨다.
구하는 값을 감소시키기 위해선 start 포인터를 우측 이동, 해당 위치의 값을 누적합에서 뺀다.
백준 2003 - 수들의 합 2
- 문제
N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오.
- 풀이
인덱스 0에서 end 포인터를 출발시킨 후 포인터 위치의 값에 따라 누적합(currentSum)을 더하거나(end 포인터 우측 이동) 빼며(start 포인터 우측 이동) 기준값(M)과 비교해가는 문제다.
투 포인터 알고리즘 자체를 구현하는 건 생각보다 어렵지 않았는데 반복문 내부 if 조건과 그 위치를 설정하는 것이 헷갈렸다.
1. 조건
① currentSum과 M이 같을 때 start 포인터 우측 이동
첫 번째 if 조건을 보면 currentSum이 M보다 클 때 뿐만 아니라 같을 때에도 start 포인터를 이동시킨다.
같을 때에는 왜 start 포인터를 이동시키는 걸까 고민했는데, 이 문제에서 수열은 자연수로 이뤄져 end 포인터를 이동해봤자 현재 currentSum 값(M과 같은 값)보다 큰 값이 나오기 때문인 것 같다. 따라서 start 포인터를 이동시켜 더 작은 값으로 만들고 다시 같은 값으로 만들어야 한다. 당연한 걸 너무 깊이 생각했나 싶다.
2. 조건 순서
② end 포인터가 인덱스 범위 밖으로 벗어날 때 break
③ currentSum이 M보다 작을 때 end 포인터 우측 이동
이 문제는 조건문의 순서도 굉장히 중요했다. 순서가 뒤바뀌면 계속 오답으로 나왔다.
1번 조건이 2번 조건보다 선행되는 이유는 end가 인덱스 끝까지 넘어갔더라도 여전히 start 포인터를 이동시켜 M과 같은 값으로 감소시킬 수 있는 경우의 수가 남아있기 때문이다. 2번 조건이 앞에 있으면 맨 마지막에 currentSum이 더 클 때 start 포인터를 이동시키면서 M과 같은 값으로 만들 기회가 사라지는 것이다.
2번 조건이 3번 조건보다 선행되어야 하는 이유는 end 값이 인덱스 범위 밖으로 벗어나게 되어 ArrayIndexOutOfBoundException 이 발생할 수 있기 때문이다.
/*
* 연속 부분수열의 합
* 입력 1 : N M (N: 정수 개수, M: 부분수열 합) (1 ≤ N ≤ 10,000, 1 ≤ M ≤ 300,000,000)
* 입력 1 : 부분수열 (자연수<=30,000)
* 출력 : 합이 M인 부분수열 개수
* */
public class Subsequence {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int num = Integer.parseInt(st.nextToken()); // 부분수열 배열 length
int sum = Integer.parseInt(st.nextToken()); // 부분수열 합
st = new StringTokenizer(br.readLine(), " ");
int[] subsequence = new int[num];
for (int i=0;i<num;i++){
subsequence[i] = Integer.parseInt(st.nextToken());
}
System.out.println(countByPointers(sum, subsequence));
}
// target 보다 크면 start++, sum-=start
// target 보다 작으면 end++, sum+=end
private static int countByPointers(int target, int[] subsequence) {
int count = 0;
int start = 0;
int end = 0;
int currentSum = 0;
while (true){
if (currentSum >= target) {
currentSum -= subsequence[start++];
} else if (end >= subsequence.length) { // 중간 => start 계속 우측 이동해 탐색 진행 & end가 인덱스 밖으로 안 넘어감
break;
} else {
currentSum += subsequence[end++];
}
if (currentSum == target) count++;
}
return count;
}
}
슬라이딩 윈도우
: 고정적인 구간을 이동시키며 값을 구하는 알고리즘

구간 길이가 변하지 않기 때문에 따로 포인터가 필요하지 않다.
겹치는 영역이 존재하므로 단계마다 해당 영역에서 제외되는 값을 빼고 추가되는 값을 더해간다.
※ TCP(전송 제어 프로토콜) 데이터 전송량 제어 => 슬라이딩 윈도우 기법 활용
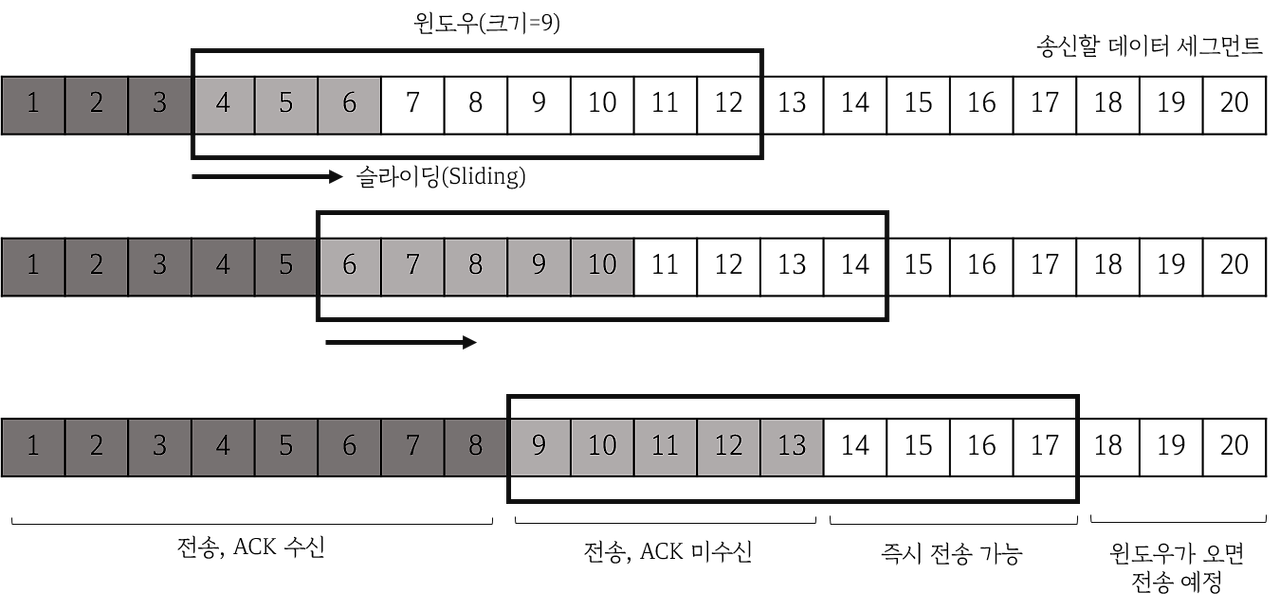
송신한 세그먼트에 대한 ACK 도착 => 그만큼 송신 윈도우에서 빠져나가고, 그만큼 새롭게 전송할 수 있는 여유 생김
(=슬라이딩 윈도우)
백준 2559 - 수열
- 문제
매일 측정한 온도가 정수의 수열로 주어졌을 때, 연속적인 며칠 동안의 온도의 합이 가장 큰 값을 계산하는 프로그램을 작성하시오.
- 풀이
start를 0, end를 start+K-1로 세팅하고 온도 합 초기값을 세팅한 후, 반복문에서 수열의 맨앞 값을 빼고 수열 뒤 값을 더해가도록 작성했다.
/*
* 온도 연속 합 최대값
* 입력 1 : N K (N: 온도 측정 날짜 수, K : 합 구하기 위한 연속된 날짜 수) (2<=N<=100000, 1<=K<=N)
* 입력 2 : 매일 측정한 온도 배열 (-100<=x<=100)
* 출력 : 온도 수열 중 K일 동안의 온도 합 최대값 출력
* */
public class Subsequence2 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int arrLength = Integer.parseInt(st.nextToken()); // 온도 측정일 수
int baseDays = Integer.parseInt(st.nextToken()); // 기준 연속일수
st = new StringTokenizer(br.readLine(), " ");
int[] temperature = new int[arrLength];
for (int i=0;i<arrLength;i++){
temperature[i] = Integer.parseInt(st.nextToken());
}
System.out.println(getMaxSum(baseDays, temperature));
}
// temperature 배열 중 baseDays 길이의 연속 수열 최대 합
private static int getMaxSum(int baseDays, int[] temperature) {
int start = 0, end = start+baseDays-1, tempSum = 0;
// 초기값 세팅
for (int i=0;i<=end;i++){
tempSum += temperature[i];
}
int max = tempSum;
// 투 포인터
while(end < temperature.length - 1){
tempSum += temperature[++end] - temperature[start++];
max = Math.max(max, tempSum);
}
return max;
}
}
심화 (슬라이딩 윈도우 + DP)
백준 2096 - 내려가기
- 문제
N줄에 0 이상 9 이하의 숫자가 세 개씩 적혀 있다. 내려가기 게임을 하고 있는데, 이 게임은 첫 줄에서 시작해서 마지막 줄에서 끝나게 되는 놀이이다.
먼저 처음에 적혀 있는 세 개의 숫자 중에서 하나를 골라서 시작하게 된다. 그리고 다음 줄로 내려가는데, 다음 줄로 내려갈 때에는 다음과 같은 제약 조건이 있다. 바로 아래의 수로 넘어가거나, 아니면 바로 아래의 수와 붙어 있는 수로만 이동할 수 있다는 것이다.
별표는 현재 위치이고, 그 아랫 줄의 파란 동그라미는 원룡이가 다음 줄로 내려갈 수 있는 위치이며, 빨간 가위표는 원룡이가 내려갈 수 없는 위치가 된다. 숫자표가 주어져 있을 때, 얻을 수 있는 최대 점수, 최소 점수를 구하는 프로그램을 작성하시오. 점수는 원룡이가 위치한 곳의 수의 합이다.
- 풀이
DP와 슬라이딩 윈도우는 생각지 못한 조합이라 열심히 다른 분들의 풀이를 보며 배웠다. 사실 처음엔 이게 왜 슬라이딩 윈도우이지 싶기도 했는데 유튜브 풀이 영상을 보고 이해했다.
온라인 알고리즘은 데이터들을 저장하지 않고 입력만 받으며 바로바로 연산 처리하는 알고리즘이며, 슬라이딩 알고리즘도 그 기법에 해당한다. 나는 슬라이딩 알고리즘을 이해할 때 윈도우라는 고정된 구간의 형태만 중시했는데, 저장 없이 입력값을 바로 처리하는(슬라이딩하는) 속성도 있음을 기억해야겠다. 아무튼 이번 문제에서는 1차원 DP 메모이제이션 배열을 만들어 입력값 행렬을 한 행씩 슬라이딩해가며 갱신한다. (i-1행의 값을 이용해 i행의 값을 갱신)
이 문제는 초기값을 세팅한 후 찾은 규칙(점화식)으로 1차원 배열 값을 갱신해가면 된다. (갱신 전 값을 미리 변수에 저장해야 하는 점도 기억해야 한다.) 문제 그림을 참고했을 때 계속 위 행 기준으로 점화식을 세우려고 했는데 (arr[0][0] → arr[1][0], arr[1][1]) 식이 제대로 세워지지 않았었다. 생각해보니 위 행의 값을 받아 아래 행을 만들어 가는 문제이므로 아래 행 기준으로 (arr[0][0], arr[0][1] → arr[1][0] ) 점화식을 세워야 했다.
쉽게 이해한 것처럼 적은 것 같은데 풀이 여러 개를 참고해가며 겨우 이해하며 풀어본 문제였다. 알고리즘은 풀면 풀수록 재밌고 막막하다.. 최대한 많은 알고리즘을 익히고 이해하고 풀어야겠다.
/*
* N행 3열 내려가기 - 아래, 대각선으로만 이동하며 누적합 최소값, 최대값 구하기
* 입력 1 : N
* 입력 2 : 행렬
* 출력 : 최대값 최소값
* */
public class Downward {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
// sliding window 알고리즘으로 갱신해갈 dp 배열
int[] maxArr = new int[3];
int[] minArr = new int[3];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int num0 = Integer.parseInt(st.nextToken());
int num1 = Integer.parseInt(st.nextToken());
int num2 = Integer.parseInt(st.nextToken());
if (i == 0) { // 초기값 세팅
maxArr[0] = minArr[0] = num0;
maxArr[1] = minArr[1] = num1;
maxArr[2] = minArr[2] = num2;
} else {
// max
int originalMax0 = maxArr[0], originalMax2 = maxArr[2];
maxArr[0] = Math.max(maxArr[0], maxArr[1]) + num0; // DP[i][0] = Math.max(DP[i-1][0], DP[i-1][1]) + newInput[i][0]
maxArr[2] = Math.max(maxArr[1], maxArr[2]) + num2;
maxArr[1] = Math.max(Math.max(originalMax0, maxArr[1]), originalMax2) + num1;
// min
int originalMin0 = minArr[0], originalMin2 = minArr[2];
minArr[0] = Math.min(minArr[0], minArr[1]) + num0;
minArr[2] = Math.min(minArr[1], minArr[2]) + num2;
minArr[1] = Math.min(Math.min(originalMin0, minArr[1]), originalMin2) + num1;
}
}
bw.write(Math.max(maxArr[0], Math.max(maxArr[1], maxArr[2])) + " ");
bw.write(Math.min(minArr[0], Math.min(minArr[1], minArr[2])) + "\n");
bw.flush();
bw.close();
br.close();
}
}
'Programming > 알고리즘' 카테고리의 다른 글
| 이분 탐색 (0) | 2024.03.09 |
|---|---|
| [백준/자바] dp 1010번 - 다리 놓기 (0) | 2024.03.09 |
| [백준/자바] 이분탐색 2805번 - 나무 자르기 (0) | 2024.03.06 |
| [백준/자바] 백트래킹 9663번 - N-Queen (0) | 2024.02.21 |
| [백준/자바] dp 11053번 - 가장 긴 증가하는 부분 수열 (0) | 2024.02.17 |


